Uzaydaki Lagrange Noktaları Nedir, Ne İşe Yarar?

Lagrange Noktaları Nedir?
Kütlesi olan her cisim bir çekim kuvveti uygular. Dünya’nın, Ay’ın, Güneş’in ve diğer bütün gök cisimlerinin kütlelerine göre uyguladıkları bir kütle çekim kuvveti vardır. Ancak uzayda bu çekim kuvvetlerinin birbirini dengelediği çok nadir noktalar bulunur. Lagrange Noktaları denilen bu noktalarda, iki büyük nesnenin kütle çekim kuvveti, küçük bir nesnenin kendileriyle birlikte hareket etmesi için gereken merkezcil kuvvete tam olarak eşittir. Uzaydaki bu faydalı noktalar, uzay araçları tarafından, daha kararlı bir yörüngede kalmak için gereken yakıt tüketimini azaltmak için kullanılmaktadır.
Lagrange Noktaları, Güneş ve Dünya gibi iki cismin çekim kuvvetleriyle oluşturduğu geniş alanlara yayılan çekim ve itim noktalarıdır. Bu alanlar, uzay araçlarının yakıt tasarrufu yapmasını sağlayabilecek görevler üstlenebilirler.
Lagrange Noktaları’nın adı, İtalyan-Fransız astronom ve matematikçi Josephy-Louis Lagrange’dan gelmektedir. Çünkü bu noktalar, Lagrange’ın ödül kazanan ve 1772’de yayımlanan Essai sur le Probléme des Trois Corps (3 Nesne Problemi Üzerine) makalesinde ele alınmıştır.

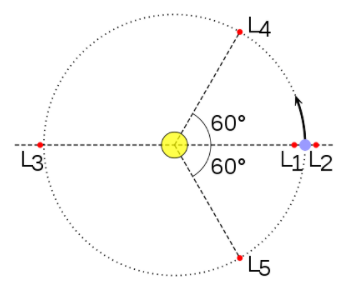
Toplamda beş önemli Langrange Noktası vardır. Bu noktalar L₁, L₂, L₃, L₄ ve L₅ olarak adlandırılmıştır. Bu noktalarda küçük bir nesne, kendisinden çok daha büyük iki nesne ile şaşmaz bir yörünge üzerinde hareket edebilir. Lagrange Noktaları’nda, iki büyük nesnenin çekim kuvveti tam olarak birbirini dengeler ve bu denge küçük bir nesnenin onlarla beraber hareket etmesini sağlayacak şartları oluşturur.

Bu beş Lagrange Noktası’ndan üçü değişkenlik gösterirken, ikisi sabit olarak tespit edilmiştir. Değişkenlik gösteren Lagrange Noktaları L₁, L₂, ve L₃ olarak adlandırılmıştır ve iki büyük nesnenin bağlantı noktasında bulunur. Sabit Lagrange Noktaları L₄ ve L₅ olarak adlandırılmıştır ve büyük kütleli iki nesneye de eşit uzaklıkta bir eş kenar üçgen oluşturur ve bu üçgenin tepesinde bulunurlar. Dünya için Güneş-Dünya ve Dünya-Ay ikilisi olmak üzere beşer adet Langrange Noktası bulunmaktadır.

Lagrange Noktaları ve Özellikleri

L₁ Noktası

Bir nesne Güneş’e ne kadar yakınsa, o kadar hızlı hareket eder. Yani, Dünya’nınkinden daha küçük bir yörüngede Güneş’in etrafında dönen herhangi bir uzay aracı nihai olarak Dünya’yı geçer. Lakin bir istisna var: Eğer uzay aracı tam olarak Dünya ve Güneş’in ortasına yerleştirilirse, Dünya’nın yerçekimi onu ters yönde çeker ve Güneş’in çekişinin bir kısmını yok sayar. Eğer mesafe tam olarak ayarlandıysa – Dünya’nın Güneş’e olan uzaklığını yaklaşık yüzde biri- uzay aracı Güneş ile Dünya arasındaki konumunu koruyacak şekilde yavaş gidecektir. Bu noktanın adı L₁’dir ve Güneş’ten gelen sabit parçacık akışı olan güneş rüzgârı, Dünya’ya ulaşmasından yaklaşık 1 saat önce L₁’e ulaştığı için Güneş’i izlemek için iyi bir konumdur. Güneş’i gözlemleyen meşhur SOHO Uzay Aracı bu noktada konumlandırılmıştır.

L₁ noktası aşağıdaki formülle hesap edilebilir. Bu ve diğer formüllerde M₁ küçük cismin kütlesini, M₂ ise büyük cismin kütlesini ifade eder. r küçük cisimden uzaklığı, R ise büyük cisimden uzaklığı ifade eder.

L₂ Noktası

L₁’in oluşmasına neden olan benzer bir etki, Dünya’nın yörüngesinin ötesinde, Dünya’nın “gece” tarafında da meydana gelir. O noktaya yerleştirilen bir uzay aracı Güneş’ten daha uzaktadır ve bu nedenle yörüngesinde Dünya’ya göre daha yavaş dönecektir. Ancak gezegenimizin fazladan çekişi Güneş’inkine katkıda bulunur ve uzay aracının Dünya’ya ayak uydurarak daha hızlı hareket etmesini sağlar. L₂, Güneş’ten bakıldığında Dünya’nın doğrudan 1,5 milyon kilometre “arkasında” yer almaktadır.

L₂, geniş bir çerçeveden, evreni gözlemlemek için mükemmel bir yerdir. Bu noktadaki bir uzay gemisinin Dünya’nın yörüngesine girmesi gerekmiyor ve bu sayede gezegenimizin gölgesine girip çıkmak, ısınmak ve soğumak bir problemi yoktur. Avrupa Uzay Ajansı’nın (ESA) bu bölgeyi kullanan birkaç uzay görevi bulunmaktadır: Herschel, Plank ve Gaia.

L₂ noktası aşağıdaki formül kullanılarak hesaplanabilmektedir.

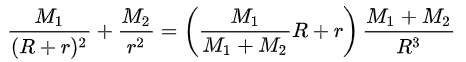
L₃ Noktası

L₃, Güneş’in arkasında, Dünya’nın karşısında, gezegenimizin yörüngesinin hemen ötesinde yer alır. L₃’teki nesneler Dünya’dan görülemez. Güneş’in uzak tarafını gözlemleme potansiyeli sunar.

L₁, L₂ veya L₃ noktasındaki bir uzay aracı, bir tepenin üzerinde duran bir top gibidir. Küçük bir itme veya sarsıntı, topu hemen hareket ettirecektir. Bu nedenle, Lagrange noktasındaki bir uzay aracının yörüngede kalması için devamlı olarak roket ateşlemesine ihtiyacı vardır.

L₃ noktası aşağıdaki formül kullanılarak hesaplanabilmektedir.

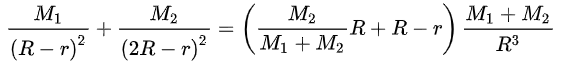
L₄ ve L₅ Noktaları

Güneş’ten görüldüğü gibi, L₄ ve L₅ noktaları, Dünya’nın,  Dünya yörüngesine yakın olarak, 60 derece önünde ve arkasında yer alır. Diğer Lagrange noktalarının aksine, L₄ ve L₅ noktaları yerçekimi bozulmalarına karşı dirençlidir. Bu sağlamlık nedeniyle, toz ve asteroitler gibi nesneler bu bölgelerde birikme eğilimindedir. Bu noktalara “Truva Noktaları” da denir.

Lagrange Noktalarını Kullanan Uzay Araçları

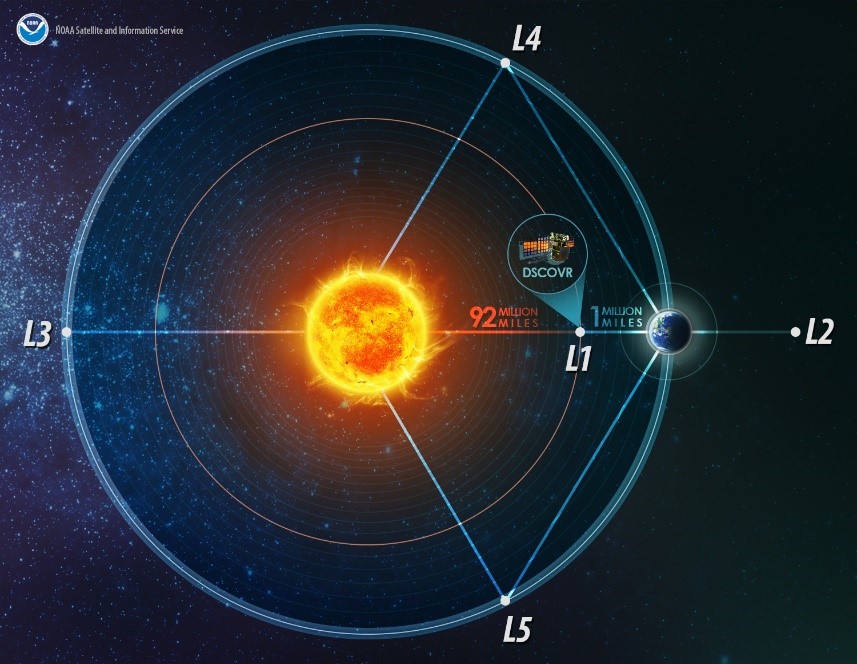
Yukarıda da bahsedildiği gibi uzay araçları Lagrange Noktalarını kullanarak daha kararlı yörüngelere oturtulabildiği için Lagrange noktalarının gök mekaniği açısından önemi büyüktür. Hem Güneş-Dünya ikilisi hem de Dünya-Ay ikilisi için beşer adet Lagrange Noktası bulunduğunu söylemiştik. Ancak uzay araçları daha çok Güneş-Dünya Lagrange Noktalarını kullanmaktadır. Güneş-Dünya Lagrange Noktaları’ndan da en çok L₁ ve L₂ noktası kullanılmaktadır. SOHO ve DSCOVR uzay araçları L₁’i,  Gaia WMAP, Herschel Uzay Gözlemevi L₂’yi, OSIRIS-REx ve STEREO A L₄’ü, Spitzer Uzay Teleskobu, Hayabusa-2 ve STEREO B de L₅’i kullanan uzay araçları olarak sıralayabiliriz. Hubble Uzay Teleskobu’nun yerini alacak meşhur James Webb Uzay Teleskobu da önümüzdeki aylarda diğer uzay araçları gibi L₂ noktasında yerini alacak. Yine NASA’nın Artemis Programı kapsamında inşa edeceği Gateway Ay İstasyonu da Lagrange Noktası’nda yerini alacak. Sonuç olarak Lagrange Noktaları uzay görevlerinde geçmişte ve şu anda kullanıldığı gibi gelecekte de kullanılmaya devam edilecek.

Kaynakça

http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/lagpt.html 

https://www.britannica.com/science/Lagrangian-point 

https://en.wikipedia.org/wiki/List_of_objects_at_Lagrange_points  

https://solarsystem.nasa.gov/resources/754/what-is-a-lagrange-point/